gnuplot /gallery / func1

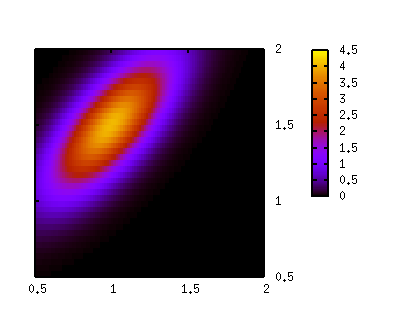
 # # Suppose we have two measured values, X and Y, with statistical errors # of 10 %. This measured quantities also have a common systematic error # of 0.2 (absolute error). The probability density function can be expressed # by a bivariate Gaussian distribution which has a center value of X and Y # with variances of 0.1*X+0.2 and 0.1*Y+0.2, respectively. #  # Measured values for quantities X and Y mx = 1.0 my = 1.5  # Uncertainties in measured X and Y (both 10%) sigx = 0.1 * mx sigy = 0.1 * my  # Common error sc = 0.2  # Total errors sx = sqrt(sigx*sigx + sc*sc) sy = sqrt(sigy*sigy + sc*sc)  # Correlation c = sc*sc/sx/sy  g(x,m,s) = (x-m)/s f(x,y,c) = exp(-1/(2*sqrt(1-c*c))* (  g(x,mx,sx)**2 -2*c*g(x,mx,sx)*g(y,my,sy) +g(y,my,sy)**2))/(2*pi*sx*sy*sqrt(1-c*c))  unset surface set view 0,0 set format z "" unset ztics set isosample 40,40 set size square set xrange [0.5:2] set yrange [0.5:2] set xtics 0.5 set ytics 0.5 set pm3d  splot f(x,y,c)