gnuplot / spherical_harmonics / deformed

Deformed Nucleus (Legendre Expansion)

[ver.4] ONLY !

The spherical harmonics Y[lm](theta,phi) is reduced to a simple
Legendre function p[l](cos(theta)) scaled by a constant when m=0,
which is independent of phi. The following equations and figure are
Y[l](theta) for several l-values.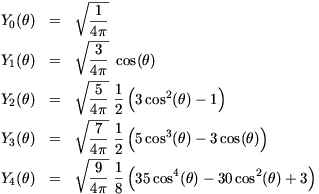

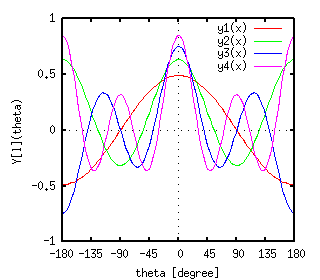
Using this Y[l](theta) with l=lambda=even terms, shape of a deformed
nucleus can be expanded as follows: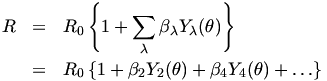

where the beta a parameter of deformation. If beta=0, the nucleus is
spherical. The 3-dim. shape given by this equation is shown with
gnuplot. As it is already shown in the previous section, we express the (x,y,z)
coordinate with the angles u,v and radius r.

x = R(theta)*cos(u)*cos(v)
y = R(theta)*sin(u)*cos(v)
z = R(theta)*sin(v)

where the theta is the angle measured from the Z-axis, so that the relation
between theta and v is theta = pi/2-v. To draw the surface,
the parameters u,v are varied from 0 to 360 deg. In the case of
beta_2 = 0.3, beta_4 = 0.1, and R_0 = 1:

gnuplot> set parametric

dummy variable is t for curves, u/v for surfaces
gnuplot> set angle degree
gnuplot> set urange [0:360]
gnuplot> set vrange [0:360]
gnuplot> set isosample 16,16
gnuplot> set ticslevel 0
gnuplot> set view 75,25
gnuplot> set size 0.7,1.0
gnuplot> set xrange [-2:2]
gnuplot> set yrange [-2:2]
gnuplot> set zrange [-2:2]
gnuplot> set urange [0:360]
gnuplot> set vrange [0:360]
gnuplot> y0(t)=1.0
gnuplot> y2(t)=sqrt(5.0/(4*pi))*( 3.0*cos(t)**2 -  1.0             )/2.0
gnuplot> y4(t)=sqrt(9.0/(4*pi))*(35.0*cos(t)**4 - 30*cos(t)**2 +3.0)/8.0
gnuplot> b2=0.3
gnuplot> b4=0.1
gnuplot> r(t) = 1 + b2*y2(0.5*pi-t) + b4*y4(0.5*pi-t)
gnuplot> fx(u,v)=cos(u)*cos(v)
gnuplot> fy(u,v)=sin(u)*cos(v)
gnuplot> fz(v)=sin(v)
gnuplot> set pm3d
gnuplot> splot r(v)*fx(u,v),r(v)*fy(u,v),r(v)*fz(v) with lines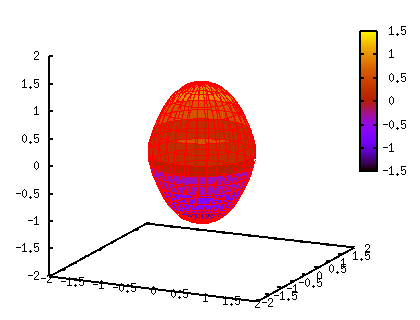

The deformation parameters, beta_2 and beta_4 can be positive or
negative. Here are some examples for some combinations of beta_2
and beta_4. The beta_2 parameters are taken to be -0.4 or 0.4, and
for each beta_2, we changed the beta_4 value from -0.2 to 0.2. When
beta_2 is positive the shape of nucleus is prolate, while it
becomes oblate if beta_2 is negative.

gnuplot> set border 0
gnuplot> unset xtics
gnuplot> unset ytics
gnuplot> unset ztics
gnuplot> unset colorbox
gnuplot> b2 = -0.4 ; b4 = -0.2 ; replot ; pause -1
gnuplot> b2 = -0.4 ; b4 =  0.0 ; replot ; pause -1
gnuplot> b2 = -0.4 ; b4 =  0.2 ; replot ; pause -1
gnuplot> b2 =  0.4 ; b4 = -0.2 ; replot ; pause -1
gnuplot> b2 =  0.4 ; b4 =  0.0 ; replot ; pause -1
gnuplot> b2 =  0.4 ; b4 =  0.2 ; replot ; pause -1